Continuous Functions on Excluded Point Topology Constant or F a B
Introduction
W. Sierpiński [20], K. Kuratowski [18] and other authors studied the possibility of defining a topological space in terms of the set of limit points. This idea was generalized by N. F. G. Martin [19] and H. Hashimoto [14]. They disscussed so called later Hashimoto type topologies (\(\star \) topologies) which were defined with the use of ideals [14] or filters [19]. Some improvements of the known results and applications of this notion were presented in 1990 by D. Janković and T. R. Hamlett [16].
Let us recall the definition of the Hashimoto topology. Let \(( X,\mathcal {T})\) be a \(T_1\) topological space, \(\mathcal {I}\) be an ideal of subsets of X which contains all singletons and \(\mathcal {I}\cap \mathcal {T}=\{ \emptyset \}\). The family \(\mathcal {H}=\{U\setminus I:U\in \mathcal {T}\wedge I\in \mathcal {I}\}\) is a base of a topology. If we additionally assume that \((X, \mathcal {T})\) is second-countable topological space and \(\mathcal {I}\) is a \(\sigma \)-ideal, then \(\mathcal {H}\) is a topology, called the Hashimoto topology. The spaces \((X, \mathcal {T})\) and \((X, \mathcal {H})\) are not homeomorphic. \((X, \mathcal {H})\) is not regular, it does not satisfy the first countability axiom, any compact set in this topology is finite and the families of connected subsets in \((X, \mathcal {T})\) and in \((X, \mathcal {H})\) coincide (for details of proofs see [19] and [14]) .
In our paper we will consider the Hashimoto topologies defined for the natural topology \(\mathcal {T}_{nat}\) and some \(\sigma \)-ideal \(\mathcal {I}\). We denote it by \({\mathcal {H}}(\mathcal {I})\) to emphasize the dependence on the ideal:
$$\begin{aligned} {\mathcal {H}}(\mathcal {I})=\{A\subset \mathbb {R}:A=U\setminus I, \text { where } U\in \mathcal {T}_{nat} \wedge I\in \mathcal {I}\}. \end{aligned}$$
Obviously, for any \(\sigma \)-ideal \(\mathcal {I}\)
$$\begin{aligned} \mathcal {T}_{nat}\subset {\mathcal {H}}(\mathcal {I}). \end{aligned}$$
(1)
It is easy to observe that any closed set in this topology (\(\mathcal {H}(\mathcal {I})\)-closed set) is of the form \(F\cup I\), where F is closed in the natural topology and \(I\in \mathcal {I}\).
We will assume that a considered \(\sigma \)-ideal \(\mathcal {I}\) has some additional properties: it is invariant with respect to dilatations and translations, which means that if \(A\in \mathcal {I}\) then \(aA\in \mathcal {I}\) and \(A+a\in \mathcal {I}\) for any \(a\in \mathbb {R}\). Such a \(\sigma \)-ideal will be called admissible.
Let us take any admissible ideal \(\mathcal {I}\) and consider continuous functions from \([0,1]\) into \(\mathbb {R}\) with the natural topology or the Hashimoto topology \(\mathcal {H}(\mathcal {I})\) on the domain and on the range. The family \(\mathcal {C}_{nat, \mathcal {H}(\mathcal {I})}\) of all continuous functions \(f:([0,1],\mathcal {T}_{nat} ) \rightarrow (\mathbb {R}, {\mathcal {H}}(\mathcal {I}))\) coincides with the family of all constant functions (it follows from the fact that for continuous function f the image of any closed interval is connected and compact in \(\mathcal {H}(\mathcal {I})\), so it is a singleton). In [19] Martin showed that under the assumption that \((Y,\mathcal {T}_Y)\) is regular the families of continuous functions from \((X, \mathcal {H})\) into \((Y,\mathcal {T}_Y)\) and from \((X, \mathcal {T})\) into \((Y,\mathcal {T}_Y)\) are equal. Therefore, for any \(\sigma \)-ideal \(\mathcal {I}\) the family \(\mathcal {C}_{\mathcal {H}(\mathcal {I}), nat}\) of all continuous functions \(f:([0,1], {\mathcal {H}}(\mathcal {I})) \rightarrow (\mathbb {R}, \mathcal {T}_{nat})\) coincides with the family of all continuous functions \(\mathcal {C}_{[0,1]}\) with the natural topology on both: their domain and range (we will call them shortly continuous).
\(\mathcal {H}(\mathcal {I})\)-continuous Functions
We will focus on the continuous functions \(f:[0,1]\rightarrow \mathbb {R}\) with the same Hashimoto topology \({\mathcal {H}}(\mathcal {I})\) on the domain and on the range of the functions. Let us denote the family of all such functions by \(\mathcal {C}_{\mathcal {H}(\mathcal {I})}\) and call them \(\mathcal {H}(\mathcal {I})\)-continuous. We will examine these families for different admissible ideals. From the fact that \(\mathcal {C}_{\mathcal {H}(\mathcal {I}), nat}=\mathcal {C}_{[0,1]}\) and (1) we obtain
$$\begin{aligned} \mathcal {C}_{\mathcal {H}(\mathcal {I})}\subset \mathcal {C}_{[0,1]}. \end{aligned}$$
(2)
It is obvious that for any admissible ideal \(\mathcal {I}\), any affine function \(f(x)=ax+b\) for \(a, b\in \mathbb {R}\) is \(\mathcal {H}(\mathcal {I})\)-continuous.
Observation 1
Let \((a_n)_{n\in \mathbb {N}}\) be a sequence such that \(0<\ldots<a_n<\ldots a_1<a_0=1 \). Assume that a continuous function \(f:[0,1]\rightarrow \mathbb {R}\) is affine on each interval \([a_{n}, a_{n-1}]\), \(n\in \mathbb {N}\), (it will be called piece-wise affine). If f is constant only on a finite number of intervals \([a_n, a_{n-1}]\) then it is \({\mathcal {H}}(\mathcal {I})\)-continuous for any admissible ideal \(\mathcal {I}\).
Observation 2
Assume that \(\mathcal {I}\) is any adsmissible ideal, \(A\subset \mathbb {R}\). If there is a limit point \(a_0\) of A such that \(a_0\notin A\) and there is a sequence \((A_n)_{n\in \mathbb {N}}\) of subsets of A such that \(A_n\notin \mathcal {I}\) and \(A_n\rightarrow a_0\) (i.e. \(\sup \{ |x-a_0|:x\in A_n \} \rightarrow 0\)), then A is not \(\mathcal {H}(\mathcal {I})\)-closed. In particular, if \(A_n\) are proper intervals then A is not \(\mathcal {H}(\mathcal {I})\)-closed for any admissible ideal \(\mathcal {I}\).
Indeed, if A is \(\mathcal {H}(\mathcal {I})\)-closed then it is of the form \(A=B\cup I\), where B is closed in the natural topology and \(I\in \mathcal {I}\). If \(a_0\notin A\), then \(a_0\notin B\) and \(\text {dist}(a_0, B)>0\). So in the neighbourhood of \(a_0\) the set \(A\setminus B\) contains a set not belonging to \(\mathcal {I}\), which is impossible as \(A\setminus B\in \mathcal {I}\).
In the paper we will use the notion of interval set, so let us recall it.
Definition 3
An interval set converging to \(x_0\) from the right is the set given by the formula \(A=\bigcup \limits _{n=1}^\infty [a_n, b_n],\) where \(x_0<\ldots<b_{n+1}<a_n<b_n< \ldots<a_1<b_1, \ n\in \mathbb {N}\), and \(\lim \limits _{n\rightarrow \infty } b_n=x_0\). Analogously we define an interval set converging to \(x_0\) from the left. Instead of closed intervals we can take the open ones.
Example 4
There exists a function \(F_1:[0,1]\rightarrow \mathbb {R}\) which is continuous but not \({\mathcal {H}}(\mathcal {I})\)-continuous for any admissible ideal \(\mathcal {I}\).
Let \(A=\bigcup _{n\in \mathbb {N}} [a_n, b_n]\) be an interval set converging to zero from the right. Let us take any sequence \((c_n)_{n\in \mathbb {N}}\) strictly decreasing and converging to zero. We define a continuous function \(F_1:[0,1]\rightarrow \mathbb {R}\) by the formula:
$$\begin{aligned} F_1(x)={\left\{ \begin{array}{ll}0 &{} \text {for } x=0\\ c_n &{} \text {for } x\in [a_n, b_n], \ n\in \mathbb {N}, \\ \text {affine}&{} \text {for } x\in [b_{n+1}, a_n], \ n\in \mathbb {N}. \end{array}\right. } \end{aligned}$$
(3)
It is evident that \(F_1\) is continuous. On the other hand it is not \({\mathcal {H}}(\mathcal {I})\)-continuous. Indeed, let us consider the set \(Y=\{c_n:n \in \mathbb {N}\}\). It is a countable set so it is closed in \({\mathcal {H}}(\mathcal {I})\), but by Observation 2 its preimage \(F_1^{-1}(Y)=\bigcup _{n\in \mathbb {N}} [a_n, b_n]\) is not closed.
By \(non\mathcal {C}_{{\mathcal {H}}}\) we will denote the family of all continuous functions which are not \({\mathcal {H}}(\mathcal {I})\)-continuous for any admissible ideal \(\mathcal {I}\).
Theorem 5
There exists a function \(F\in non\mathcal {C}_{{\mathcal {H}}}\) such that for any \(a\ne 0\) the function \(F_a=F+a\cdot {{\,\mathrm{id}\,}}\) is \({\mathcal {H}}(\mathcal {I})\)-continuous for any admissible ideal \(\mathcal {I}\).
Proof
To obtain F we slightly modify the function \(F_1\) from the previous example. For a given interval set \(A=\bigcup (a_n, b_n)\) converging to zero from the right we choose the sequence \((c_n)_{n\in \mathbb {N}}\) in the following way:
- 1.
\(c_1=1\)
- 2.
\(c_{n+1}<c_n\) for \(n\in \mathbb {N}\),
- 3.
all slopes of the straight lines on \([b_{n+1}, a_n]\) are different .
Let us consider the function \(F_a=F+a\cdot {{\,\mathrm{id}\,}}\) with \(a\ne 0\). Then \(F_a\) may be constant on at most one interval \([b_{n+1}, a_n]\). So according to Observation 1 it is \({\mathcal {H}}(\mathcal {I})\)-continuous.
From the above theorem we can easyly obtain the next corollary.
Corollary 6
No family \(\mathcal {C}_{\mathcal {H}(\mathcal {I})}\) is closed under addition.
Proof
Let F be the function constructed in Theorem 5, put \(f(x)=x\) and \(g(x)=F(x)-x\). Then f and g are \({\mathcal {H}}(\mathcal {I})\)-continuous but their sum is not \({\mathcal {H}}(\mathcal {I})\)-continuous.
In the paper [9] there is introduced the notion of linearly sensitive functions. A function f is called linearly sensitive with respect to the property (P) if f has the property (P) and for any \(a\ne 0\) the function \(f+a\cdot {{\,\mathrm{id}\,}}\) does not have the property (P). By \(\mathcal {S}(P)\) we will denote the family of all functions linearly sensitive with the respect to the property (P). Theorem 5 may be written in the form: \(\mathcal {S}(non\mathcal {C}_{{\mathcal {H}}})\ne \emptyset \).
Theorem 7
The set \(\mathcal {S}(non\mathcal {C}_{{\mathcal {H}}})\) is dense in \(\mathcal {C}_{[0,1]}\).
Proof
Let us consider \(\mathcal {C}_{[0,1]}\) with the metric supremum. Let us fix a function f continuous on \([0,1]\) and \(\varepsilon \in (0, 1)\). From the uniform continuity of f it follows that there exists \(\delta >0\) such that \(|f(x)- f(z)|<\varepsilon \) for any \(x,z\in [0,1]\) for which \(|x-z|<\delta \). The unit interval \([0,1]\) is the union of finite number of closed itervals \(I_n\), \(n=1, \ldots , k\), each of the length less than \(\delta \). Then the length of each \(J_n=[\min _{x\in I_n}f(x), \max _{x\in I_n}f(x)]\) is less than \(\varepsilon \). Let us take any point \(x_0\) from the interior of \(I_1\) and a number \(\varepsilon _1<\varepsilon \) such that \(S_1=(x_0-\varepsilon _1, x_0+\varepsilon _1)\times (f(x_0)-\varepsilon _1, f(x_0)+\varepsilon _1)\subset I_1\times J_1\). For the sequence \((c_n)_{n\in \mathbb {N}}\) such that \(c_1<f(x_0)+\varepsilon _1\), in the square \(S_1\) we construct a copy of the function F from Theorem 5. In the intervals \(I_n\), \(n\ge 2\), we approximate f with piece-wise affine functions \(f_n\) with different slopes and such that \(d(f, f_n)<\varepsilon \). Let
$$\begin{aligned} g(x)={\left\{ \begin{array}{ll} F(x) &{} \text {for }x\in (x_0-\varepsilon _1, x_0+\varepsilon _1) ,\\ f_n(x)&{} \text {for }x\in I_n, n=1, \ldots , k,\\ \text {affine} &{} \text {for }x\in I_1\setminus (x_0-\varepsilon _1, x_0+\varepsilon _1) \end{array}\right. } \end{aligned}$$
so that the obtained function g is continuous. From the construction we have \(g\in \mathcal {S}(non\mathcal {C}_{{\mathcal {H}}})\). Moreover, \(d(f, g)<\varepsilon \) which means, that \(\mathcal {S}(non\mathcal {C}_{{\mathcal {H}})})\) is dense in \(\mathcal {C}_{[0,1]}\). \(\square \)
\(\mathcal {H}(\mathcal {I})\)-continuous Functions for Frequently used \(\sigma \)-ideals
For the first time the notion of an ideal was used in the XIXth century in the algebra, namely in the ring theory. The family \(\mathcal {I}\) of subsets of a commutative ring \(\mathcal {P}\) is called ideal if for any a,b belonging to \(\mathcal {I}\) their difference \(a-b\) belongs to \(\mathcal {I}\) and for any \(a\in \mathcal {I}\) and \(b\in \mathcal {P}\) the product ab belongs to \(\mathcal {I}\). It was observed that by identifying \( \mathcal {P}\) with the set of so called principial ideals of the form \(\mathcal {I}_a=\{ ab:b\in \mathcal {P}\}\) we can treat the set of ideals in \(\mathcal {P}\) as the extension of \(\mathcal {P}\). The nonprincipal elements of such an extension were called the ideal elements, shortly ideals. The set of ideals, principial or not, (with appropriate algebraic operations) forms a new ring in some sense more regular then the original one. If we consider a Boolean ring \(\mathcal {P}(X)\), for some nonempty set X, with the symmetric difference and intersection as the operations (or, what is equivalent, a Boolean algebra \(\mathcal {P}(X)\) with "\(\cup \)" and "\(\cap \)"), we observe that a family of sets \(\mathcal {I}\) is an ideal in \(\mathcal {P}(X)\) if it is closed under finite unions and taking subsets. Such properties should be owned by the families of sets, we want to call small. Hence, the mathematicians have been using the notion of ideal (\(\sigma \)-ideal) of sets in many fields whenever they want to say that a certain property holds for almost all elements. What does it mean for almost all? Now we say for all except the set belonging to some ideal (\(\sigma \)-ideal). The best known admissible \(\sigma \)-ideals of subsets of \(\mathbb {R}\) are: the \(\sigma \)-ideal of countable sets \(\mathcal {I}_{\omega }\), the \(\sigma \)-ideal \(\mathcal {N}\) of sets of the Lebesgue measure zero and the \(\sigma \)-ideal \(\mathcal {K}\) of meager sets (the first category sets). In this section we will examine the families \(C_{\mathcal {H}(\mathcal {I})}\) for each of them.
It is worth noting that for any continuous function f and any admissible ideal \(\mathcal {I}\)
-
if \(f^{-1}(A)\in \mathcal {I}\) for any \(A\in \mathcal {I}\) then \(f\in \mathcal {C}_{\mathcal {H}(\mathcal {I})}\),
-
\(f\not \in \mathcal {C}_{\mathcal {H}(\mathcal {I})}\) if and only if there exists a set \(A\in \mathcal {I}\) such that \(f^{-1}(A)\) is not closed in \(\mathcal {H}(\mathcal {I})\).
In particular any continuous injection is \(\mathcal {H}(\mathcal {I}_{\omega })\)-continuous. Moreover, it is also \(\mathcal {H}(\mathcal {K})\)-continuous. It can be derived from the fact that for such function preimage of countable (nowhere dense) set is also countable (nowhere dense).
It follows from Observation 1 that \(\bigcap _{\mathcal {I}} C_{\mathcal {H}(\mathcal {I})}\ne \emptyset \). In the next theorem we present an unexpected result concerning the family \(C_{\mathcal {H}(\mathcal {K})}\).
Theorem 8
If f belongs to \( \mathcal {C}_{\mathcal {H}(\mathcal {I})}\) for an admissible ideal \(\mathcal {I}\) then f belongs to \( \mathcal {C}_{\mathcal {H}(\mathcal {K})}\). In other words \(\bigcup _{\mathcal {I}} C_{\mathcal {H}(\mathcal {I})}= \mathcal {C}_{\mathcal {H}(\mathcal {K})}\).
Proof
We will show in the proof that if \(f\notin \mathcal {C}_{\mathcal {H}(\mathcal {K})}\) then \(f\notin \mathcal {C}_{\mathcal {H}(\mathcal {I})}\).
Firstly we will prove that if a continuous function f is not constant on any interval, then it is \(\mathcal {H}(\mathcal {K})\)-continuous. Let us assume contrary that \(f\notin C_{\mathcal {H}(\mathcal {K})}\). Then there exists \(\mathcal {H}(\mathcal {K})\)-closed set whose preimage is not \(\mathcal {H}(\mathcal {K})\)-closed. As f is continuous, the preimage of any closed set is closed in the natural topology. So there exists a set \(A\in \mathcal {K}\) such that \(f^{-1}(A)\) is of the second category. Hence we have a nowhere dense set \(B\subset A\) for which \(f^{-1}(B)\) is not nowhere dense. The closure \(\overline{B}\) is nowhere dense and \(f^{-1}(\overline{B})\) contains an interval J (as a closed set of the second category). From continuity of f it follows that f(J) is connected so it is either a singleton or an interval. It can not be an interval because \(f(J)\subset \overline{B}\), so it is a singleton which gives a contradiction.
Let us fix an arbitrary continuous function f and denote by \(\mathcal {F}\) the family of all intervals \(I_n=[a_n, b_n]\) such that f is constant on \(I_n\). Let \(Y=\{f(I_n): n\in \mathbb {N}\}\). If Y is finite, then repeating the previous reasonning we obtain that \(f\in \mathcal {C}_{\mathcal {H}(\mathcal {K})}\). Indeed, if \(f\notin \mathcal {C}_{\mathcal {H}(\mathcal {K})}\) then there exist a nowhere dense set \(\overline{B}\) disjoint with Y and an interval J such that \(J\subset f^{-1}(\overline{B})\). Then \(f(J)\subset \overline{B}\), so f(J) is a singleton. Hence \(f(J)\in Y\), a contradiction.
Let us assume now that Y is infinite. It is bounded so it contains a sequence \((y_n)_{n\in \mathbb {N}}\) converging to some point \(y_0\). For any \(n\in \mathbb {N}\) there is an interval \( I_n\in \mathcal {F}\) such that \(f(I_n)=y_n\). Intervals \((I_n)_{n\in \mathbb {N}}\) are disjoint and their left ends \(a_n\) form a sequence convergent to some \(x_0\). From continuity of f it follows that \(f(x_0)=y_0\). The set \(Y\setminus \{y_0\}\) is closed but \(f^{-1}(Y\setminus \{y_0\})\) is not closed in \(\mathcal {H}(\mathcal {I})\) so, by Observation 2, f is not \(\mathcal {H}(\mathcal {I})\)-continuous for any admissible ideal \(\mathcal {I}\). \(\square \)
Even if the admissible ideals \(\mathcal {I}_1\) and \(\mathcal {I}_2\) are comparable, we can not compare the families of continuous functions \(C_{\mathcal {H}(\mathcal {I}_1)}\) and \(C_{\mathcal {H}(\mathcal {I}_2)}\) (see Example 9 and Example 10). However, \(\mathcal {C}_{ \mathcal {H}(\mathcal {I})}\subset \mathcal {C}_{\mathcal {H}(\mathcal { I\cap K})}\) for any admissible ideal \(\mathcal {I}\). Indeed, let us suppose that \(f\in \mathcal {C}_{\mathcal {H}(\mathcal {I})}\) and fix a set \(A\in \mathcal {I\cap K}\). Since \(f\in \mathcal {C}_{\mathcal {H}(\mathcal {I })}\), \(f^{-1}\left( A\right) \in \mathcal {I}\). By Theorem 7, \(f^{-1}\left( A\right) \in \mathcal {K}\).
Example 9
There exists a function \(F_2\in \mathcal {C}_{\mathcal {H}(\mathcal {I}_{\omega })}\setminus \mathcal {C}_{\mathcal {H}(\mathcal {N})}\). Consequently, \(F_2\in \mathcal {C}_{\mathcal {H}(\mathcal {K})}\setminus \mathcal {C}_{\mathcal {H}(\mathcal {N})}\).
Let C be the Cantor ternary set and let \(f_c\) be the Cantor function. Let us consider the function \(g(x)=f_c(x)+x\). Then \(g:[0,1]\rightarrow \mathbb {R}\) is strictly increasing. So the inverse function \(F_2=g^{-1}\) is also strictly increasing, hence it is \(\mathcal {H}(\mathcal {I}_{\omega })\)-continuous. We will show that it is not \(\mathcal {H}(\mathcal {N})\)-continuous. Since \(\lambda (g(C))=1\) (\(\lambda \) stands for the Lebesgue measure on the real line), the set g(C) contains a nonmeasurable subset A. Take \(B\subset C\) such that \(g(B)=A\). Then B is closed (as a set from the ideal \(\mathcal {N}\)) and its preimage \(F_2^{-1}(B)=g(B)\) is not closed because it is nonmeasurable. Hence \(F_2\notin \mathcal {C}_{\mathcal {H}(\mathcal {N})}\).
Another example of a function with the desired properties is the strongly singular function which will be used in Theorem 19.
Example 10
There exists a function \(F_3\in \mathcal {C}_{\mathcal {H}(\mathcal {N})}\setminus \mathcal {C}_{\mathcal {H}(\mathcal {I}_{\omega })}\). Consequently, \(F_3\in \mathcal {C}_{\mathcal {H}(\mathcal {K})}\setminus \mathcal {C}_{\mathcal {H}(\mathcal {I}_{\omega })}\).
Let C be the Cantor ternary set and \(\bigcup _{n=1}^{\infty }(a_n,b_n)\) be its complement to [0, 1]. Let f be the auxiliary function defined by the formula:
$$\begin{aligned} f(x)={\left\{ \begin{array}{ll} x-a_n&{}\text {for }x\in (a_n, \frac{a_n+b_n}{2}), n\in \mathbb {N},\\ -x+b_n&{}\text {for }x\in (\frac{a_n+b_n}{2}, b_n), n\in \mathbb {N},\\ 0&{}\text {for }x\in C. \end{array}\right. } \end{aligned}$$
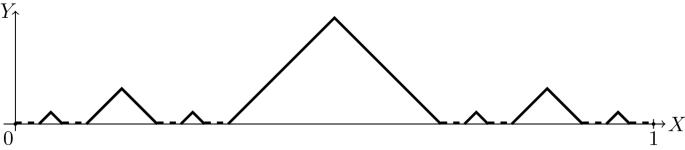
Auxiliary function f from Example 10
Evidently f is continuous. It is also \(\mathcal {H}(\mathcal {N})\)-continuous. Let us take any set \(N\in \mathcal {N}\). Then its preimage is also of measure zero. Indeed, if \(0\in N\) then \(f^{-1}(\{0\})=C\). The preimage of the set \(N\setminus \{0\}\) cuts only a denumerable number of intervals \((a_n, b_n)\). On those intervals f is an affine function so the set \(f^{-1}(N\setminus \{0\})\) has measure zero. Hence \(f^{-1}(N)\) is of measure zero and \(f\in \mathcal {C}_{\mathcal {H}(\mathcal {N})}\). From Theorem 8 we obtain \(f\in \mathcal {C}_{\mathcal {H}(\mathcal {K})}\).
Let us take any interval set \(U=\bigcup _{n=1}^{\infty } (u_n, v_n)\) converging to zero from the right and a sequence of positive terms \((c_n)_{n\in \mathbb {N}}\) decreasing to zero such that \(c_{n}-c_{{n+1}}> \frac{v_{n+1}-u_{n+1}}{6}\) for \(n\in \mathbb {N}\). On each level \(y=c_n\), we construct a copy of the function f defined on the interval \([u_n, v_n] \). On intervals \((v_{n+1}, u_n)\) we have straight lines so that the obtained function \(F_3\) is continuous. Then \(F_3^{-1}(\{c_n\})\) is a Cantor set. Denote it \(C^{(n)}\). The function \(F_3\) is not \(\mathcal {H}(\mathcal {I}_{\omega })\)-continuous, because the preimage of the set \(Y=\{c_n:n\in \mathbb {N}\}\in \mathcal {I}_{\omega }\) is equal to \(F_3^{-1}(Y)=\bigcup _n C^{(n)}\) and is not closed in \(\mathcal {H}(\mathcal {I}_{\omega })\) (by Observation 2). We show that \(F_3\) is \(\mathcal {H}(\mathcal {N})\)-continuous anologously as in the case of auxiliary function f.
Let us observe that by slight modification in the definition of \(F_3\) we can construct a function which is \(\mathcal {H}(\mathcal {K})\)-continuous, but neither \(\mathcal {H}(\mathcal {I}_{\omega })\)-continuous nor \(\mathcal {H}(\mathcal {N})\)-continuous.
Example 11
There exists a function \(F_4\in \mathcal {C}_{\mathcal {H}(\mathcal {K})}\setminus \big (\mathcal {C}_{\mathcal {H}(\mathcal {I}_{\omega })}\cup \mathcal {C}_{\mathcal {H}(\mathcal {N})}\big )\).
Proof
We construct the desired function \(F_4\) in the same way as in the Example 10, but we use the Cantor set \(\widehat{C}\) of positive measure instead of the Cantor ternary set. It is sufficient to show that \(F_4\in \mathcal {C}_{\mathcal {H}(\mathcal {K})}\setminus \mathcal {C}_{\mathcal {H}(\mathcal {N})}\).
Since f is not constant on any interval, then \(f\in \mathcal {C}_{\mathcal {H}(\mathcal {K})}\) by the first part of the proof of Theorem 8.
We prove that \(f\notin \mathcal {C}_{\mathcal {H}(\mathcal {N})}\) in a similar way as it is done in the last part of the previous proof. Let \(Y=\{c_n:n\in \mathbb {N}\}\). Then \(F_4^{-1}(\{c_n\})=\widehat{C}_{(n)}\) is a Cantor set of positive measure included in the interval \([u_n, v_n] \), \(n\in \mathbb {N}\). Then Y is \(\mathcal {H}(\mathcal {N})\)-closed but by Observation 2 the set \(F_4^{-1}(Y)=\bigcup _n \widehat{C}_{(n)}\) is not \(\mathcal {H}(\mathcal {N})\)-closed, so \(F_4\notin \mathcal {C}_{\mathcal {H}(\mathcal {N})}\). \(\square \)
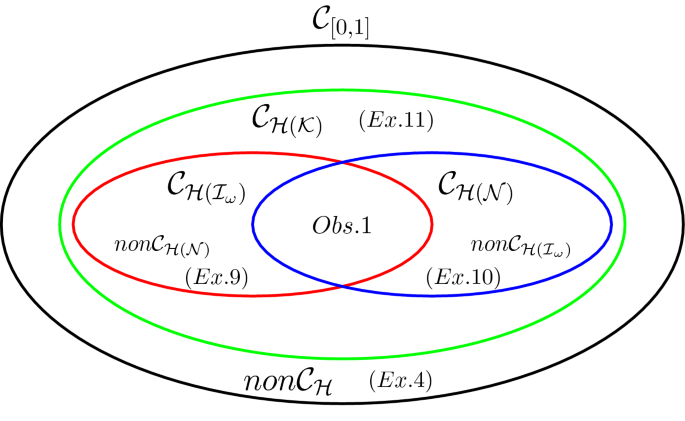
The figure below presents all obtained results related to the mutual dependencies between considered families.
Algebrability
In the last few years the question whether the family of functions having some special properties contains a large algebraic structure became important. This problem is connected with so-called lineability and algebrability of sets in function spaces. It is particularly interesting if the considered family is not closed with respect to some algebraic operations.
This research began with the papers [1, 2] (the wider survey one can find in [3, 12]). In algebrability one of the first results were connected with the space of everywhere surjective functions [4] and the space of continuous functions which are nowhere differentiable [11]. The authors have proved that such function spaces contain the infinitely generated algebras. Let us take a cardinal \(\kappa \). We will say that a subset A of a commutative algebra is \(\kappa \)-algebrable if \(A\cup \{0\}\) contains a \(\kappa \)-generated algebra B, i.e. the minimal cardinality of a set of generators of B is equal to \(\kappa \). If \(\kappa =\omega \) then we will shortly say that A is algebrable. In [10] A. Bartoszewicz and S. Gła̧b introduced the notion of strong algebrability which do not coincides with the algebrability. Following them, we say that A is strongly \(\kappa \)-algebrable if \(A\cup \{0\}\) contains a \(\kappa \)-generated algebra B that is isomorphic with the free algebra. Denoting by \(X=\{x_{\alpha }:\alpha <\kappa \}\) the set of generators of the free algebra B, we obtain that the set of elements of the form \(x_{\alpha _1}^{k_1}x_{\alpha _2}^{k_2}\dots x_{\alpha _n}^{k_n}\) is linearly independent and all linear combinations of such elements are in \(A\cup \{0\}\). A useful and not difficult criterion of strong \(\mathfrak {c}\)-algebrability was presented by M. Balcerzak, A. Bartoszewicz and M. Filipczak in [7]. Their technique, called the exponential-like functions method will be used in this section. Many applications of this method can be found in [8].
Definition 12
We say that a function \(f:\mathbb {R}\rightarrow \mathbb {R}\) is exponential-like of rank m if it is given by the formula \(f(x)=\sum \limits _{i=1}^{m}a_i e^{\beta _i x}\) for some distinct nonzero numbers \(\beta _1, \ldots ,\beta _m\) and some nonzero real numbers \(a_1, \ldots ,a_m\).
The following property of the exponential-like functions is very helpful and we will apply it in a few proofs.
Property 13
[Lemma 8, [7]] For every positive integer m, any exponential-like function \(f:\mathbb {R}\rightarrow \mathbb {R}\) of rank m, and each \(c\in \mathbb {R}\), the preimage \(f^{-1}\left[ \{c\}\right] \) has at most m elements. Consequently, f is not constant in every subinterval of \(\mathbb {R}\).
It is evident that any exponential-like function f belongs to \(C^{\infty }\) and \(f'\) is an exponential-like function, too. So in the face of Property 13, f has a finite number of extremes attained at points \(x_1\), ...\(x_k\). Putting \(x_0=0\) and \(x_{k+1}=1\) we have that the restriction \(f|_{[x_i, x_{i+1}]}\) is strictly monotone for any \(i=0, \ldots , k\).
In this section we will use the nice criterion of the strong \(\mathfrak {c}\)-algebrability formulated in the following theorem.
Theorem 14
[Proposition 7, [7]] Given a family \({\mathcal F}\subset \mathbb {R}^{[0,1]}\), assume that there exists a function F such that \(f\circ F\in {\mathcal F}\setminus \{0\}\) for every exponential-like function \(f : \mathbb {R}\rightarrow \mathbb {R}\). Then \({\mathcal F}\) is strongly \(\mathfrak {c}\)-algebrable. More exactly, if \(H\subset \mathbb {R}\) is a set of cardinality \(\mathfrak {c}\), linearly independent over the rationals \(\mathbb {Q}\), then \(\mathrm {exp}\circ (rF)\), \(r\in H\), are free generators of an algebra contained in \({\mathcal F}\cup \{0\}\).
It is easy to see that in the above theorem instead of exponential-like function we can use any algebra which is isomorphic with a free algebra of \(\mathfrak {c}\) generators.
Theorem 15
Any exponential-like function belongs to \( \mathcal {C}_{\mathcal {H}(\mathcal {J}_{\omega })}\cap \mathcal {C}_{\mathcal {H} (\mathcal {N})}\).
Proof
By Property 13 for any denumerable set A its preimage \(f^{-1}\left( A\right) \) is also denumerable, so \(f\in \mathcal {C}_{\mathcal {H}(\mathcal {J}_{\omega })}\).
Let us fix a null set N and denote by \(x_1\), ...\(x_k\) the points at which f attaines its extremes. It is sufficient to check that for any \(i=0, \ldots , k\) the set \(f^{-1}(N)\cap (x_i, x_{i+1})\) is of measure zero. Let us fix \(i\in \{0, \ldots , k\}\) and denote by \(([a_j, b_j])_{j\in \mathbb {N}}\) a sequence of intervals such that
$$\begin{aligned} \bigcup \limits _{j=1}^{\infty }\left[ a_{j},b_{j}\right] =\left( x_{i},x_{i+1}\right) . \end{aligned}$$
For any j, \(f|_{[a_j,b_j]}\) is strictly monotone. Let us assume that it is increasing and denote \(\left[ c_{j},d_{j}\right] :=f\left( \left[ a_{j},b_{j}\right] \right) \). Let us consider \(\left( f|_{\left[ a_{j},b_{j}\right] } \right) ^{-1}\). Since \(f'\left( x\right) >0\) for any \( x\in \left[ a_{j},b_{j}\right] \), then \(\left( f|_{\left[ a_{j},b_{j}\right] } \right) ^{-1}\) is defined and continuous on \(\left[ c_{j},d_{j} \right] \) and \(\left( f|_{\left[ a_{j},b_{j}\right] }\right) ^{-1}:\left[ c_{j},d_{j}\right] \rightarrow \left[ a_{j},b_{j}\right] \). The function \(\left( f|_{\left[ a_{j},b_{j}\right] }\right) ^{-1}\) has bounded derivative, so it fulfills the Lipschitz condition. From that and the equality
$$\begin{aligned} \lambda \left( f^{-1}\left( N\right) \cap \left[ a_j,b_{j}\right] \right) =\lambda \left( f^{-1}\left( N\cap \left[ c_{j},d_{j}\right] \right) \right) =0 \end{aligned}$$
we have
$$\begin{aligned} \lambda \left( f^{-1}\left( N\right) \cap \left( x_{i},x_{i+1}\right) \right) \le \sum \limits _{j=1}^{\infty }\lambda \left( f^{-1}\left( N\right) \cap \left[ a_{j},b_{j}\right] \right) =0. \end{aligned}$$
Therefore, \(f\in \mathcal {C}_{\mathcal {H} (\mathcal {N})}\).
Corollary 16
The family \(\mathcal {C}_{\mathcal {H}(\mathcal {J}_{\omega })}\cap \mathcal {C}_{\mathcal {H}(\mathcal {N})}\) is strongly \(\mathfrak {c}\)-algebrable.
Directly from Theorem 14 and Example 4 it follows:
Theorem 17
The family \(non\mathcal {C}_{\mathcal {H}}=\mathcal {C}_{[0,1]}\setminus \bigcup \mathcal {C}_{\mathcal {H}(\mathcal {I})}\) is strongly \(\mathfrak {c}\)-algebrable.
Proof
Let \(F_1\) be the function described in Example 4 given by the formula (3), and let f be arbitrary exponential-like function. Then \(f\circ F_1\) is constant on the intervals \(\left[ a_{n},b_{n}\right] \) and the set \(\left\{ (f\circ F_1)\left( \left[ a_{n},b_{n}\right] \right) :n\in \mathbb {N}\right\} \) is infinite. Therefore, by Observation 2, \(f\circ F_1\notin \bigcup \mathcal {C}_{\mathcal {H}(\mathcal {I})}\). \(\square \)
Theorem 18
The family \(\mathcal {C}_{\mathcal {H}(\mathcal {N} )}\setminus \mathcal {C}_{\mathcal {H}(\mathcal {J}_{\omega })}\) is strongly \(\mathfrak {c}\)-algebrable.
Proof
Let us take the function \(F_3\) from Example 10. Then there exists a denumerable set \(Y=\left\{ c_{n}:n\in \mathbb {N}\right\} \) such that for any \(n\in \mathbb {N}\) the set \(F_3^{-1}(\left\{ c_{n}\right\} )\in \mathcal {N}\setminus \mathcal {J} _{\omega }\).
Let f be any exponential-like function. The set \(Z:=f(Y)\) is denumerable, but \(\left( f\circ F_3\right) ^{-1}\left( Z\right) \supset F_3^{-1}(Y) \notin \mathcal {J}_{\omega }\) and it is not \(\mathcal {H}(\mathcal {I}_{\omega })\)-closed, so by Example 10, \(f\circ F_3\notin \mathcal {C}_{\mathcal {H}( \mathcal {J}_{\omega })}\).
Both functions f and \(F_3\) are from the class \(\mathcal {C}_{\mathcal {H}(\mathcal {N})}\) so \( f\circ F\in \mathcal {C}_{\mathcal {H}(\mathcal {N})}\) which completes the proof. \(\square \)
Theorem 19
The family \(\mathcal {C}_{\mathcal {H}(\mathcal {K})}\setminus \left( \mathcal {C}_{\mathcal {H}(\mathcal {I}_{\omega })}\cup \mathcal {C}_{\mathcal {H}(\mathcal {N})}\right) \) is strongly \(\mathfrak {c}\)-algebrable.
Proof
Let us consider the function \(F_4\) from Example 11. For any exponential-like function f after repeating the reasoning from the previous proof we conclude that \(f\circ F_4\not \in \mathcal {C}_{\mathcal {H}(\mathcal {I}_{\omega })}\) and \(f\circ F_4\not \in \mathcal {C}_{\mathcal {H}(\mathcal {N})}\). From Theorem 15 we have \(f\in \mathcal {C}_{\mathcal {H}(\mathcal {K})}\). Since \(F_4\in \mathcal {C}_{\mathcal {H}(\mathcal {K})}\), then \(f\circ F_4\in \mathcal {C}_{\mathcal {H}(\mathcal {K})}\). \(\square \)
Theorem 20
The family \(\mathcal {C}_{\mathcal {H}(\mathcal {I} _{\omega })}\setminus \mathcal {C}_{\mathcal {H}(\mathcal {N})}\) is strongly \(\mathfrak {c}\)-algebrable.
Proof
A continuous function f is called strongly singular whenever \(f'=0\) almost everywhere and f is not constant in every interval. Strictly increasing strongly singular functions are described in [21] where a good bibliography on this topic is presented. A nice example of strictly increasing strongly singular function from [0, 1] onto [0, 1] is also presented in [13, §31]. Such a function F maps some null set \(A\subset \left[ 0,1\right] \) onto a set of measure 1. Therefore, \(F\notin \mathcal {C}_{\mathcal {H}(\mathcal {N})}\) and (as injection) it is a function belonging to the class \(\mathcal {C}_{\mathcal {H}(\mathcal {I}_{\omega })}\).
Let f be an exponential-like function. Then \(f\circ F\in \mathcal {C}_{\mathcal {H}(\mathcal {I}_{\omega })}\) as a composition of two functions from \(\mathcal {C}_{\mathcal {H}(\mathcal {I}_{\omega })}\).
Let us denote \(B:=\left[ 0,1\right] \setminus f\left( A\right) \). Since F is a bijection, \(\left( F\right) ^{-1}(B)=A^{\prime }\) is a set of measure 1. Since \(B\in \mathcal {N}\) and f is absolutely continuous function, \(f(B)\in \mathcal {N}\). From Theorem 15 it follows that \(f^{-1}\left( f(B)\right) \in \mathcal {N}\). From the inclusion \(B\subset f^{-1}\left( f(B)\right) \) we have
$$\begin{aligned} A^{\prime }\subset \left( F\right) ^{-1}\left( f^{-1}\left( f(B)\right) \right) \text {.} \end{aligned}$$
Hence the set
$$\begin{aligned} \left( f\circ F\right) ^{-1}\left( f(B)\right) =F^{-1}\left( f^{-1}\left( f(B)\right) \right) \end{aligned}$$
is of full measure in \(\left[ 0,1\right] \) and it is not closed. Therefore, it is not \(\mathcal {H}(\mathcal {N})\)-closed, which proves that \(f\circ F\notin \mathcal {C}_{\mathcal {H}(\mathcal {N})}\). \(\square \)
One can ask, when algebras constructed in this section are dense in \(\mathcal {C}_{[0,1]}\). The answer to this question is that the constructed algebra is dense, if and only if the starting function F is one-to-one. Indeed, if F is one-to-one then by similar argument as in Theorem 10 in [7] the algebra is dense. On the other hand, when F is not one-to-one (i.e. it does not separate some points x and y) then any function in the algebra (even in its closure) can not separate x and y. Therefore, the algebra constructed in Theorem 19 is dense in \(\mathcal {C}_{[0,1]}\).
\(\mathcal {H}(\mathcal {I})\)-continuity for some other Ideals
There are many admissible \(\sigma \)-ideals, for which we can consider the family of \(\mathcal {H}\)-continuous functions. In this section we present a few results connected with \(\mathcal {H}(\mathcal {I})\)-continuous functions with respect to the \(\sigma \)-ideal \(\mathcal {M}\) of microscopic sets and \(\sigma \)-ideal \(H_0\) of sets of Hausdorff dimension zero.
The notion of microscopic sets on \(\mathbb {R}\) was introduced by J. Appell in [5], but the wide survey of this topic can be found in [15].
Definition 21
A set \(A\subset \mathbb {R}\) is microscopic if for each \(\varepsilon >0\) there exists a sequence of intervals \((I_n)_{n\in \mathbb {N}}\) such that \(A\subset \bigcup _{n\in \mathbb {N}} I_n \) and \(\lambda (I_n)\le \varepsilon ^n\) for any \(n\in \mathbb {N}\).
The family of microscopic sets forms a \(\sigma \)-ideal. Clearly
$$\begin{aligned} \mathcal {I}_{\omega }\subset \mathcal {M}\subset \mathcal {N}. \end{aligned}$$
Since the Cantor ternary set is not microscopic (see [6]), the second inclusion is proper. A Cantor type set (a nowhere dense perfect set) which is microscopic is constructed in [17]. It follows that the first inclusion is proper, too.
To introduce some necessary denotations and for the convenience of the reader we recall the construction of a Cantor type set which is microsopic.
Example 22
[15]. There is a nowhere dense perfect set \(C_m\) which is microscopic.
We shall define by induction the sequence of open intervals \((J_{n,i})\) with \(i=1, \ldots , 2^{n-1}\). Let \(J_{1,1}=(\frac{1}{4}, \frac{3}{4})\). By \(K_{1,1}\) and \(K_{1,2}\) we denote the successive components of \([0,1]\setminus J_{1,1}\). Evidently \(\lambda (K_{1,1})=\lambda (K_{1,2})=\frac{1}{2^{2^1}}\). In the second step by \(J_{2,1}\), \(J_{2,2}\) we denote two open intervals concentric with \(K_{1,1}\) and \(K_{1,2}\) respectively, such that \(\lambda (J_{2,1})=\lambda (J_{2,2})=\lambda (K_{1,1})-2\cdot \frac{1}{3^{2^2}}\). By \(K_{2,1}\), \(K_{2,2}\), \(K_{2,3}\), \(K_{2,4}\) we denote the succesive components of the set \([0,1]\setminus (J_{1,1}\cup J_{2,1}\cup J_{2,2})\). Then \(\lambda (K_{2,i})=\frac{1}{3^{2^2}}\) for \(i=1,2,3,4\). In each k step we have the open, nonempty intervals \(J_{k,1}, \ldots , J_{k,2^{p-1}}\) concentric with the closed intervals \(K_{k-1, 1}, \ldots , K_{k-1, 2^{k-1}}\) respectively, such that \(\lambda (J_{k,i})=\lambda (K_{k-1,1})-2\cdot \frac{1}{(k+1)^{2^k}}\) for \(i=1, \ldots , 2^{k-1}\), \(k\in \mathbb {N}\). Finally we put \(C_m=\bigcap _{k=1}^{\infty }\bigcup _{i=1}^{2^{k}}K_{k,i}\) The obtained set is perfect, nowhere dense and microscopic.
Lemma 23
Let I be an interval. Suppose that \(f:I\rightarrow \mathbb {R}\) is a strictly monotone differentiable function and there exist positive numbers M and m such that for any \(x\in I\)
$$\begin{aligned} 0<m<|f'(x)|<M. \end{aligned}$$
Then
$$\begin{aligned} A\in \mathcal {M}\Leftrightarrow f(A)\in \mathcal {M}\end{aligned}$$
for any \(A\subset I\).
Proof
For any \(x,y\in I\)
$$\begin{aligned} m|x-y|\le |f(x)-f(y)|\le M|x-y|. \end{aligned}$$
(4)
We can assume that \(M>1\) and \(m<1\). As f is a continuous bijection, f(J) is an interval for any interval \(J\subset I\), and
$$\begin{aligned} m\cdot \lambda \left( J\right) \le \lambda \left( f\left( J\right) \right) \le M\cdot \lambda \left( J\right) \end{aligned}$$
Let us fix a microscopic set \(A\subset I\) and a positive number \(\varepsilon \). Since \(A\in \mathcal {M}\), there exists a sequence of intervals \(\left( I_{n}\right) _{n\in \mathbb {N}}\) such that \(A\subset \bigcup I_{n}\) and \(\lambda \left( I_{n}\right) \le \left( \frac{\varepsilon }{M}\right) ^{n}\) for any \(n\in \mathbb {N}\). Therefore, for any \(n\in \mathbb {N}\)
$$\begin{aligned} \lambda \left( f\left( I_{n}\right) \right) \le M\cdot \lambda \left( I_{n}\right) \le M\cdot \left( \frac{\varepsilon }{M}\right) ^{n}<\varepsilon ^{n}\text {.} \end{aligned}$$
Obviously
$$\begin{aligned} f\left( A\right) \subset f\left( \bigcup I_{n}\right) =\bigcup f\left( I_{n}\right) \text {,} \end{aligned}$$
so \(f(A)\in \mathcal {M}\). Using the left inequality in (4), we obtain the second implication. \(\square \)
It is clear that the \(\sigma \)-ideal \(\mathcal {M}\) is invariant with respect to translations and dilatations (see [15]). Therefore it is an admissible \(\sigma \)-ideal and we can consider the family \(\mathcal {C}_{\mathcal {H}\left( \mathcal {M}\right) }\).
Theorem 24
The family \(\left( \mathcal {C}_{\mathcal {H}\left( \mathcal {N }\right) }\cap \mathcal {C}_{\mathcal {H}\left( \mathcal {I}_{\omega }\right) }\right) \setminus \mathcal {C}_{\mathcal {H}\left( \mathcal {M}\right) }\) is densely strongly \(\mathfrak {c}\)-algebrable.
Proof
We will start with finding a function \(F_{5}\in \left( \mathcal {C}_{\mathcal {H}\left( \mathcal {N}\right) }\cap \mathcal {C}_{ \mathcal {H}\left( \mathcal {I}_{\omega }\right) }\right) \setminus \mathcal {C} _{\mathcal {H}\left( \mathcal {M}\right) }\). Firstly we define an auxiliary function \(f:[0,1]\rightarrow [0,1]\) which belongs to the difference \(\mathcal {C}_{\mathcal {H}(\mathcal {N})}\setminus \mathcal {C}_{\mathcal {H}(\mathcal {M})}\).
Let us consider the Cantor ternary set C on x-axis, and the miscroscopic set \( C_{m}\) constructed in Example 22 on y-axis. The construction of the Cantor ternary set is well known, but we recall it shortly to enter some denotations. We start from the unit interval \([0,1]\) and we denote the middle set of the lenth \(\frac{1}{3}\) by \(E_{1,1}\). By \(L_{1,1}\) and \(L_{1,2}\) we denote the successive components of \([0,1]\setminus E_{1,1}\). In each k step we have the open, nonempty intervals \(E_{k,1}, \ldots , E_{k,2^{k-1}}\) concentric with the closed intervals \(L_{k-1, 1}, \ldots , L_{k-1, 2^{k-1}}\) respectively, such that \(\lambda (E_{k,i})= (\frac{1}{3})^k\) for \(i=1, \ldots , 2^{p-1}\), \(k\in \mathbb {N}\). The ternary Cantor set \(C=\bigcap _{k=1}^{\infty }\bigcup _{i=1}^{2^{k}}L_{k,i}\) is perfect, nowhere dense and of measure zero.
Let us take the intervals \(J_{p,i}\), \(i=1, \ldots , 2^{p-1}\), \(p\in \mathbb {N}\) from Example 22 and put: \(E_{p,i}=(a_{p,i}, b_{p,i})\) and \(J_{p,i}=(c_{p,i}, d_{p,i})\). In the first step for \([a_{1,1}, b_{1,1}]=[\frac{1}{3}, \frac{2}{3}]\) and \([c_{1,1}, d_{1,1}]=[\frac{1}{4}, \frac{3}{4}]\) we construct piece-wise affine function \(f_1\) in the following way: we put \(f_1(0)=0\), \(f_1(1)=1\), \(f_1(a_{1,1})=c_{1,1}\), \(f_1(b_{1,1})=d_{1,1}\) and \(f_1\) is affine on the intervals \([0, a_{1,1}]\) and \([b_{1,1}, 1]\). Then \(f_1\) is continuous and strictly increasing. In the second step we modify \(f_1\) in the intervals \([0,a_{1,1}]\) and \([b_{1,1}, 1]\). Let \(f_2(x)=f_1(x) \) on \([a_{1,1}, b_{1,1}]\), \(f_2(0)=0\), \(f_2(1)=1\), \(f_2(a_{2,1})=c_{2,1}\), \(f_2(b_{2,1})=d_{2,1}\), \(f_2(a_{2,2})=c_{2,2}\), \(f_2(b_{2,2})=d_{2,2}\) and affine on other intervals so that \(f_2\) is continuous and strictly increasing. Proceeding in the same way we obtain the uniformly convergent sequence \(f_n\) of continuous strictly increasing functions.
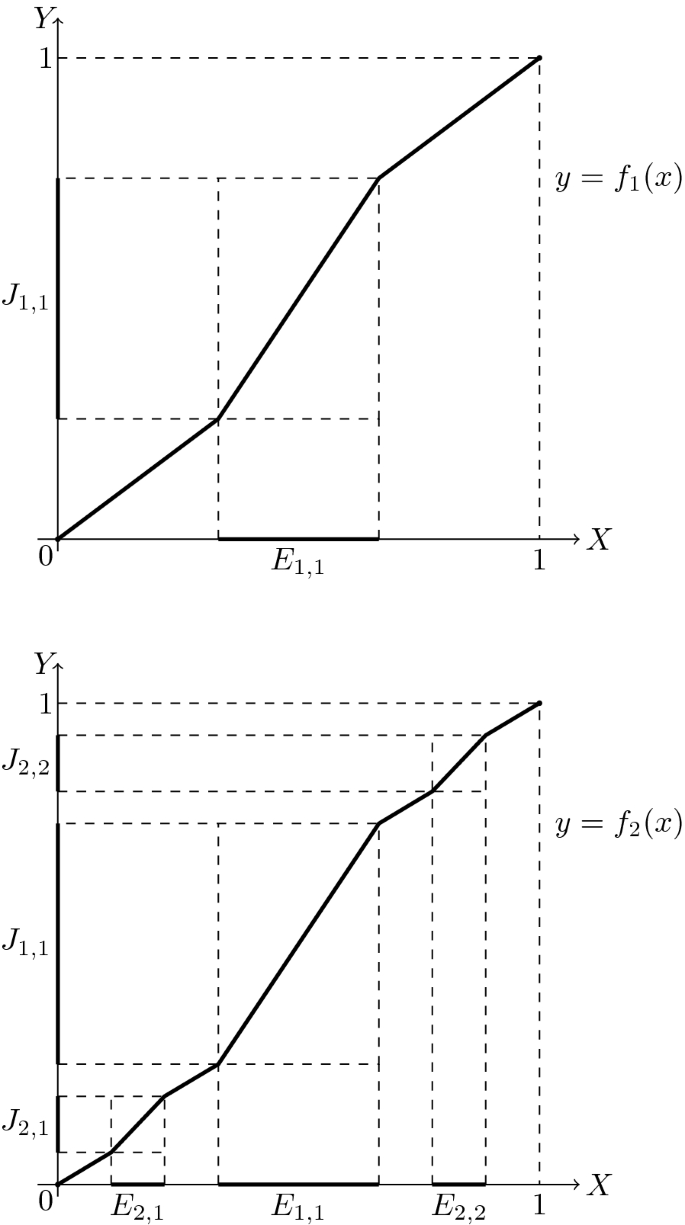
First two steps of constuction from Theorem 24
Let us put \(f=\lim _{n\rightarrow \infty }f_n\). Then f is continuous and strictly increasing, so it is \(\mathcal {H}(\mathcal {I}_{\omega })\)-continuous. Let us observe that f is also \(\mathcal {H}(\mathcal {N})\)-continuous. Take any set N of measure zero. We will show that \(f^{-1}(N)\) has also the measure zero. Consider \(N=(C_m\cap N)\cup (N\setminus C_m)\). Then \(f^{-1}(C_m\cap N)\subset C\) so it has measure zero. The set \(N\setminus C_m\) is a subset of complement of \(C_m\) and is of measure zero so its preimage under the affine function is also of measure zero. Hence \(f^{-1}(N)\) is a null set, so \(f\in \mathcal {C}_{\mathcal {H}(\mathcal {N})}\).
Next step is analogous to this presented in Theorem 10. Let us take an interval set \(U=\bigcup _{n=1}^{\infty } (u_n, v_n)\) convergent to 0 from the right and a sequence \((c_n)_{n\in \mathbb {N}}\) of positive numbers strictly decreasing to zero and such that \(c_{n}-c_{n+1}> v_{n+1}-u_{n+1}\), \(n\in \mathbb {N}\). In the same way as in Theorem 10 we construct a function \(F_5\). Let us consider the square \(W_n=[u_n,v_n]\times [u_n,v_n]\). Let \(C_m^{(n)}\) denote the microscopic set contained in \([u_n, v_n]\) on y-axis, \(C^{(n)}\) the Cantor set on x-axis. On each level \(y=c_n\) in \(W_n\) we build a copy of the function f, name it \(g_{n}\). Then \(g^{-1}_{n}(C_m^{(n)})=C^{(n)}\). Now we connect graphs of all \(g_{n}\), \(n\in \mathbb {N}\), with affine functions to have a continuous function \(F_5\).
We shall prove that \(F_5\in \mathcal {C}_{\mathcal {H}(\mathcal {N})}\setminus \mathcal {C}_{\mathcal {H}(\mathcal {M})}\). Firstly let us observe that \(F_5\notin \mathcal {C}_{\mathcal {H}(\mathcal {M})}\). Consider the set \(Y=\{C_m^{(n)}:n\in \mathbb {N}\}\). It is \(\mathcal {H}(\mathcal {M})\)-closed but its preimage is not \(\mathcal {H}(\mathcal {M})\)-closed because \(F_5^{-1}(Y)=\bigcup _n C^{(n)}\), and the set \(\bigcup _n C^{(n)}\) is not \(\mathcal {H}(\mathcal {M})\)-closed. Anologously as in the case of auxiliary function f we show that \(F_5\) is \(\mathcal {H}(\mathcal {N})\)-continuous which completes the proof. \(\square \)
To prove the strong \(\mathfrak {c}\)-algebrability of \(\left( \mathcal {C}_{ \mathcal {H}\left( \mathcal {N}\right) }\cap \mathcal {C}_{\mathcal {H}\left( \mathcal {I}_{\omega }\right) }\right) \setminus \mathcal {C}_{\mathcal {H} \left( \mathcal {M}\right) }\) we again use the the exponential-like functions method and consider functions of the form \(f\circ F_{5}\), where f is an exponential-like function. In Theorem 15 we showed that any exponential-like function belongs to \(\mathcal {C}_{\mathcal {H}\left( \mathcal {N}\right) }\cap \mathcal {C}_{\mathcal {H}\left( \mathcal {I}_{\omega }\right) }\). The function \(F_{5}\) belongs to \(\mathcal {C}_{\mathcal {H} \left( \mathcal {N}\right) }\cap \mathcal {C}_{\mathcal {H}\left( \mathcal {I} _{\omega }\right) }\) either, so \(f\circ F_{5}\in \mathcal {C}_{\mathcal {H} \left( \mathcal {N}\right) }\cap \mathcal {C}_{\mathcal {H}\left( \mathcal {I} _{\omega }\right) }\). Repeating the reasoning from the proof of Theorem 18, we obtain that \(f\circ F_{5}\notin \mathcal {C}_{\mathcal {H}\left( \mathcal {M} \right) }\).
The density of the constructed algebra in \(\mathcal {C}_{\left[ 0,1\right] } \) follows from the fact that the function \(F_{5}\) is one-to-one.
Directly from the last theorem it follows that
$$\begin{aligned} \mathcal {C}_{\mathcal {H}\left( \mathcal {N}\right) }\cap \mathcal {C}_{ \mathcal {H}\left( \mathcal {I}_{\omega }\right) }\cap \mathcal {C}_{\mathcal {H} \left( \mathcal {M}\right) }\subsetneq \mathcal {C}_{\mathcal {H}\left( \mathcal {N}\right) }\cap \mathcal {C}_{\mathcal {H}\left( \mathcal {I}_{\omega }\right) } \end{aligned}$$
Using Lemma 23 and repeating the second part of the proof of Theorem 15 we obtain that any exponential-like function belongs to \( \mathcal {C}_{\mathcal {H}\left( \mathcal {M}\right) }\). Therefore
Theorem 25
The family \(\mathcal {C}_{\mathcal {H}\left( \mathcal {N} \right) }\cap \mathcal {C}_{\mathcal {H}\left( \mathcal {I}_{\omega }\right) }\cap \mathcal {C}_{\mathcal {H}\left( \mathcal {M}\right) }\) is densely strongly \(\mathfrak {c}\)-algebrable.
Let us recall some information to introduce another \(\sigma \)-ideal connected with the measure.
Definition 26
For any set \(A\subset \mathbb {R}\), \(\delta \in (0,\infty ]\) and \(\alpha \in (0,\infty )\) we define the outer measure
$$\begin{aligned} H_{\delta }^{\alpha }(A)=\inf \Big \{ \sum \limits _{n\in \mathbb {N}}(diam A_n)^{\alpha }:A\subset \bigcup _{n\in \mathbb {N}} A_n \text { oraz diam} (A_n)<\delta \Big \}. \end{aligned}$$
The \(\alpha \)-dimensional Hausdorff measure of a set A is defined as \(H^{\alpha }(A)=\lim \limits _{\delta \rightarrow 0} H_{\delta }^{\alpha }(A).\) The Hausdorff dimension of A is a number
$$\begin{aligned} \text {dim}_H(A)=\inf \{s\ge 0:H^s(A)=0\}. \end{aligned}$$
The family of sets of the Hausdorff dimension zero forms a \(\sigma \)-ideal denoted by \(H_0\). The classical ternary Cantor set is a null set, but has positive Hausdorff dimension. In [6] there is constructed a Cantor type set \(C_{H}\) which has Hausdorff dimension 0 and is not microscopic. Hence
$$\begin{aligned} \mathcal {I}_{\omega }\subsetneq \mathcal {M}\subsetneq H_{0}\subsetneq \mathcal {N}. \end{aligned}$$
It is known that \(H_0\) is admissible, so we may consider \(\mathcal {H}\)-continuity with respect to it. By repeating the reasoning from the proof of Theorem 24 we have
Example 27
There exists functions \(F_6\in \mathcal {C}_{\mathcal {H}({H_0})}\setminus \mathcal {C}_{\mathcal {H}(\mathcal {M})}\) and \(F_7\in \left( \mathcal {C}_{\mathcal {H}(\mathcal {N})}\cap \mathcal {C}_{\mathcal {H}(\mathcal {I}_{\omega })}\right) \setminus \mathcal {C}_{\mathcal {H}({H_0})}\).
In the construction we use the same method as in Theorem 24: to have \(F_6\) we use the set \(C_H\) on x-axis and the microscopic set \(C_m\) on y-axis. To obtain \(F_7\) we put the Cantor ternary set C on x-axis and a Cantor-type set \(C_H\) of Hausdorff dimension 0 on y-axis.
We decided to show the full research on continuous functions in the Hashimoto topologies generated with the most often used \(\sigma \)-ideals: of the countable sets, of the Lebesgue measure zero sets and of the meager sets. In the last section we only touched the problem for the microscopic sets and sets of Hausdorff dimension zero. We think that similar considerations can be promising also for some other \(\sigma \)-ideals: for the \(\sigma \)-ideal of sets with the Hausdorff \(\alpha \)-dimensional measure zero for \(0<\alpha \le 1\) or the \(\sigma \)-ideals not directly related to the measure or category, for instance the \(\sigma \)-ideal of \(\sigma \)-porous sets or the \(\sigma \)-ideal of the Marczewski \(s_{0}\)-sets.
References
-
Aron, R.M., García, D., Maestre, M.: Linearity in non-linear problems. RACSAM. Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Mat. 95(1): 7–13 (2001)
-
Aron, R.M., Gurariy, V.I., Seoane-Sepúlveda, J.B.: Lineability and spaceability of sets of functions on. Proc. Amer. Math. Soc. 133(3), 795–803 (2005)
-
Aron, R.M., Bernal-Gonzáles, L., Pellegrino, D., Seoane-Sepúlveda, J.B.: Lineability: the search for linearity in mathematics. Monographs and researcg notes in mathematics. CRC Press, Boca Raton, FL (2016)
-
Aron, R.M., Seoane-Sepúlveda, J.B.: Algebrability of the set of everywhere surjective functions on \(C\). Bull. Belg. Math. Soc. Simon Stevin 14(1), 25–31 (2007)
-
Appell, J.: Insiemi ed operatori piccoli in analisi funzionale. Rend. Ist. Mat. Univ. Trieste 33, 127–199 (2001)
-
Appell, J., D Aniello, E., Väth, E.: Some remarks on small sets. Ric. Mat. 50, 255–274 (2001)
-
Balcerzak, M., Bartoszewicz, A., Filipczak, M.: Nonseparable spaceability and strong algebrability of sets of continuous singular functions. J. Math. Anal. Appl. 407(2), 263–269 (2013)
-
Bartoszewicz, A., Bienias, M., Filipczak, M., Gła̧b, Strong cont-algebrability of strong Sierpiński-Zygmund, smooth nowhere analytic and other sets of functions. 412 (2), 620–630 (2014)
-
A. Bartoszewicz, M. Filipczak, M. Terepeta, Lineability of linearly sensitive functions, Results Math. 75(2) (2020), Paper No 64, 14 pp, https://doi.org/10.1007/s00025-020-01187-3
-
Bartoszewicz, A., Gła̧b, S.: Strong algebrability of sets of sequences and functions. Proc. Amer. Math. Soc. 141(3), 827–835 (2013)
-
Bayart, F., Quarta, L.: Algebras in sets of queer functions. Israel J. Math. 158(1), 285–296 (2007)
-
Bernal-Gonzáles, L., Pellegrino, D., Seoane-Sepúlveda, J.B.: Linear subsets of nonlinear sets in topological vector spaces. Bull. Amer. Math. Soc. 51(1), 71–130 (2014)
-
Billingsley, P.: Probability and Measure. Wiley and Sons, New York (1979)
-
Hashimoto, H.: On the *topology and its application. Fund. Math. 91(1), 5–10, (1976)
-
Horbaczewska, G., Karasińska, A., Wagner-Bojakowska, E.: Properties of the \(\sigma \)- ideal of microscopic sets, in Traditional and present-day topics in real analysis, pp. 325–343. University of Lodz, Faculty of Mathematics and Computer Science (2013)
-
Janković, D., Hamlett, T.R.: New Topologies from Old via Ideals. Amer. Math. Monthly 94(4), 295–310 (1990)
-
Karasińska, A., Wagner-Bojakowska, E.: Homeomorphisms of linear and planar sets of the first category into microscopic sets. Topology Appl. 159(7), 1894–1898 (2012)
-
Kuratowski, K. Topology. Vol. I. New edition, revised and augmented Translated from the French by J. Jaworowski Academic Press, New York-London; Państwowe Wydawnictwo Naukowe, Warsaw 1966 xx+560 pp
-
Martin, N.F.G.: Generalized condensation points. Duke Math. J. 28, 507–514 (1961)
-
Sierpiński, W.: La notion de d erive comme base d thorie des ensembles abstraits. Mathematische Annalen 97, 321–337 (1927)
-
Takacs, L.: An increasing continuous singular function. Amer. Math. Monthly 85, 35–37 (1978)
Source: https://link.springer.com/article/10.1007/s00025-021-01488-1
Publicar un comentario for "Continuous Functions on Excluded Point Topology Constant or F a B"